記事の内容
Macnaughton Smith et al. (1965)が提案した分割型クラスタリングをPythonで実装しました。本記事では、そのスクリプトを公開します。
分割型クラスタリングとは
分割型クラスタリングの定義を例によってカステラ本から引きます。
分割型クラスタリング法では、全データが属する一つのクラスタから開始し、トップダウンに、一つの既存クラスタを二つの子クラスタに再帰的に各反復で分割していく。
つまり、一つの大きなクラスタを複数のクラスタに分割していく手法が分割型クラスタリングです(図1)。デンドログラムを上から作っていくイメージのクラスタリングです。
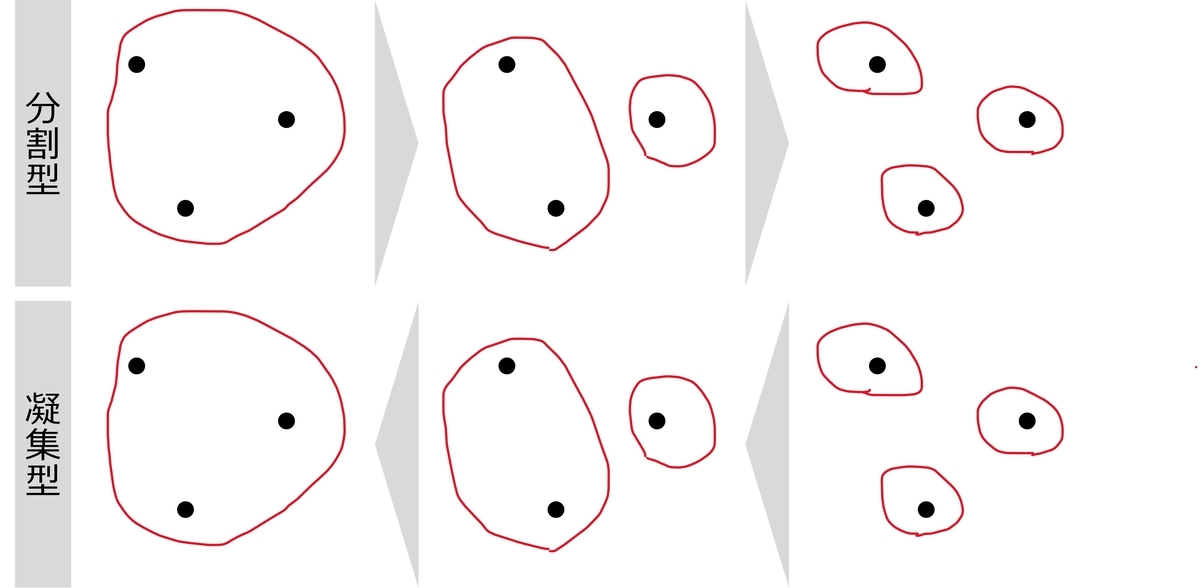
実装する手法の説明
アルゴリズムの概要
Macnaughton Smith et al. (1965)が提案したクラスタリング手法を、またまたカステラ本から引きます。
この手法では、まず全観測を一つのクラスタGに配置する。次に、他の観測との平均非類似度が最も大きい観測を選ぶ。この観測を2番目のクラスタHの最初の要素とする。続く各ステップにおいて、Gに含まれる観測のうち、Hまでの平均距離からG中の残りの観測との平均距離を引いた値が最も大きいものをHに移す。この平均の差が負になるまで、この操作を続ける。つまり、平均してH中の観測により近い観測は、Gには含まれなくなる。この結果、もとのクラスタは、Hに移した観測集合とGに残った観測集合の二つの子クラスタに分割される。(中略)その後の各階層は、前の階層のクラスタの一つにこの分割手順を適用して生成することができる。
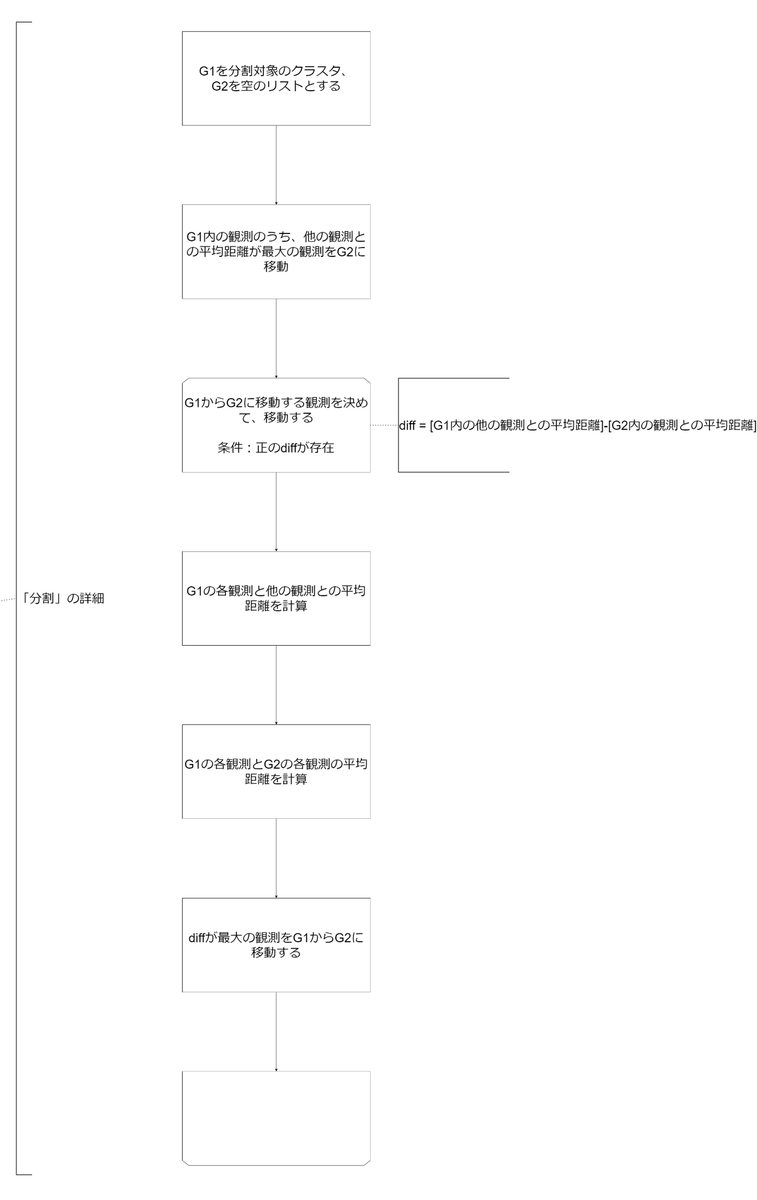
このように、文章でアルゴリズムを説明されてもわかりにくいと思うので、図に直します(図2)。
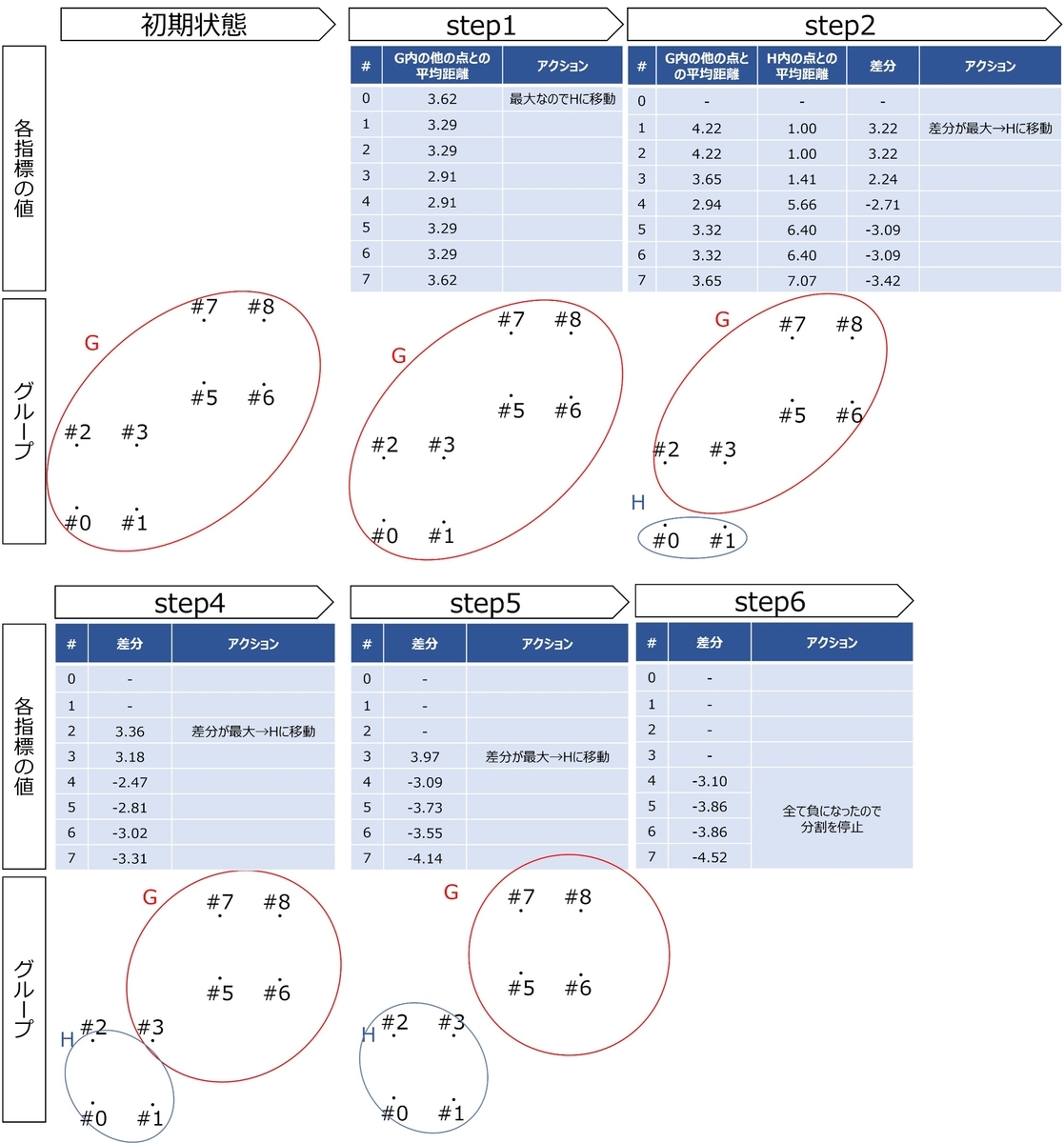
クラスタ内の他の観測と比較して離れているものを別のクラスタに移動していくイメージです。
実装!
構成
作成するスクリプトの構成は下記の通りです。

フローチャート
アルゴリズムをPythonに落とし込むためにフローチャートを作成します。
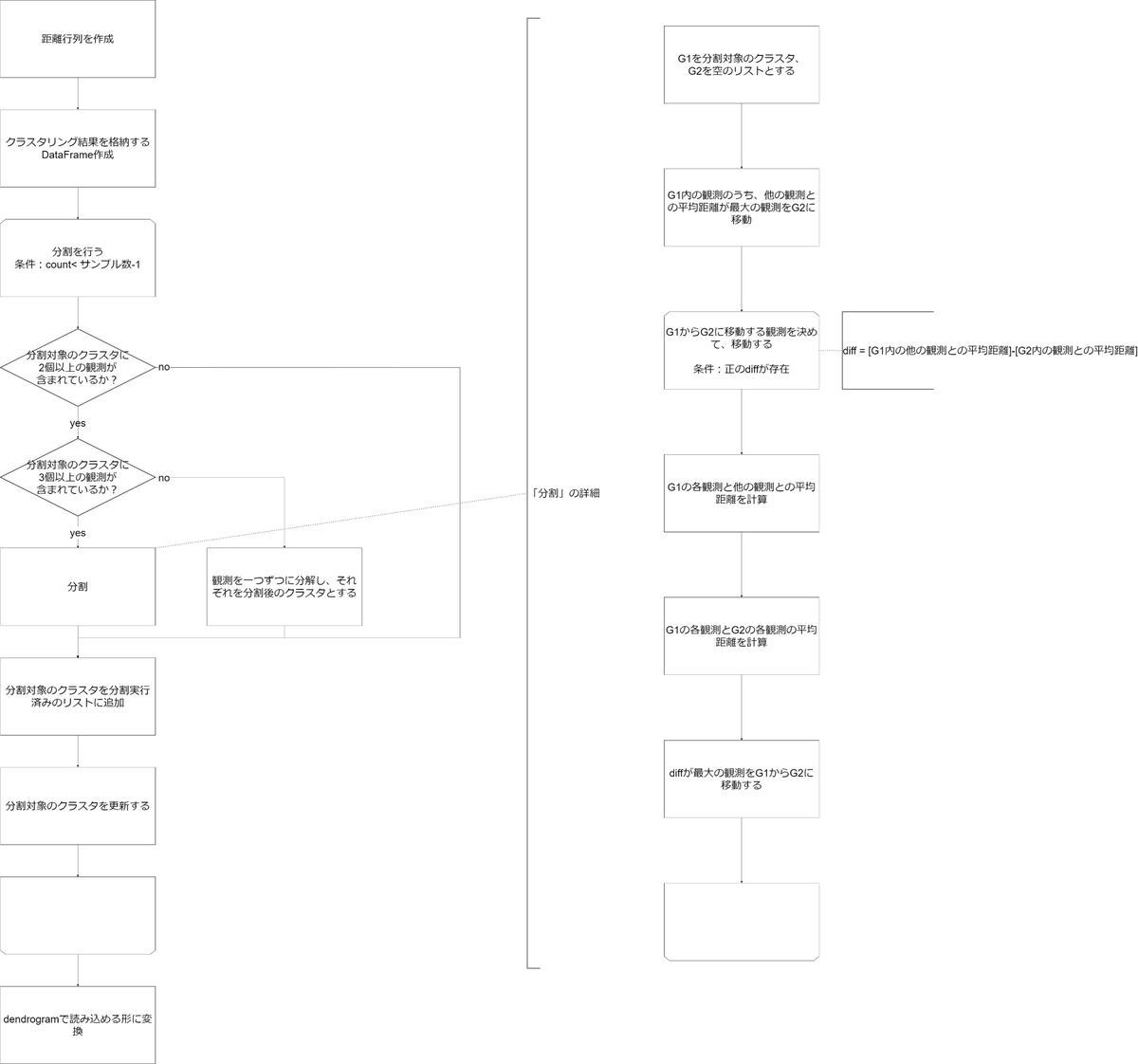
スクリプトとフローチャートの対応関係
図3のフロチャートとスクリプトの細かな対応を見ていきます。以下、フロチャート→スクリプトの順に書いていきます。
まず、距離行列を作成する箇所ですが、これはmakeDistanceMatrix関数で実現します。

# 距離行列を作成する関数 def makeDistanceMatrix(self): # 各データの組み合わせを作成 combination_df = self.df-self.df[:, np.newaxis] # 組み合わせごとに距離を計算 d_matrix = np.array([[np.linalg.norm(combination_df[i, j]) for i in range(0, len(self.df))] for j in range(0, len(self.df))]) # 出力 self.d_matrix = d_matrix return(d_matrix)
次に、クラスタリング結果を格納するDataFrame作成ですが、これについては特別なことをしていません。初期値として0行目に元のクラスタのインデックスを格納しておきます。

# クラスタリング結果を格納するDataFrame定義 tmp0_result_DF = pd.DataFrame(columns=["tmp_cluster_no", "cluster", "diff", "children"]) # 0行目は元のクラスタのインデックスを格納 tmp0_result_DF.loc[0] = [0, list(range(0, len(self.df))), np.nan, np.nan]
さらに本命の分割をする部分です。ここはいくつかの関数に分けて実現しました。
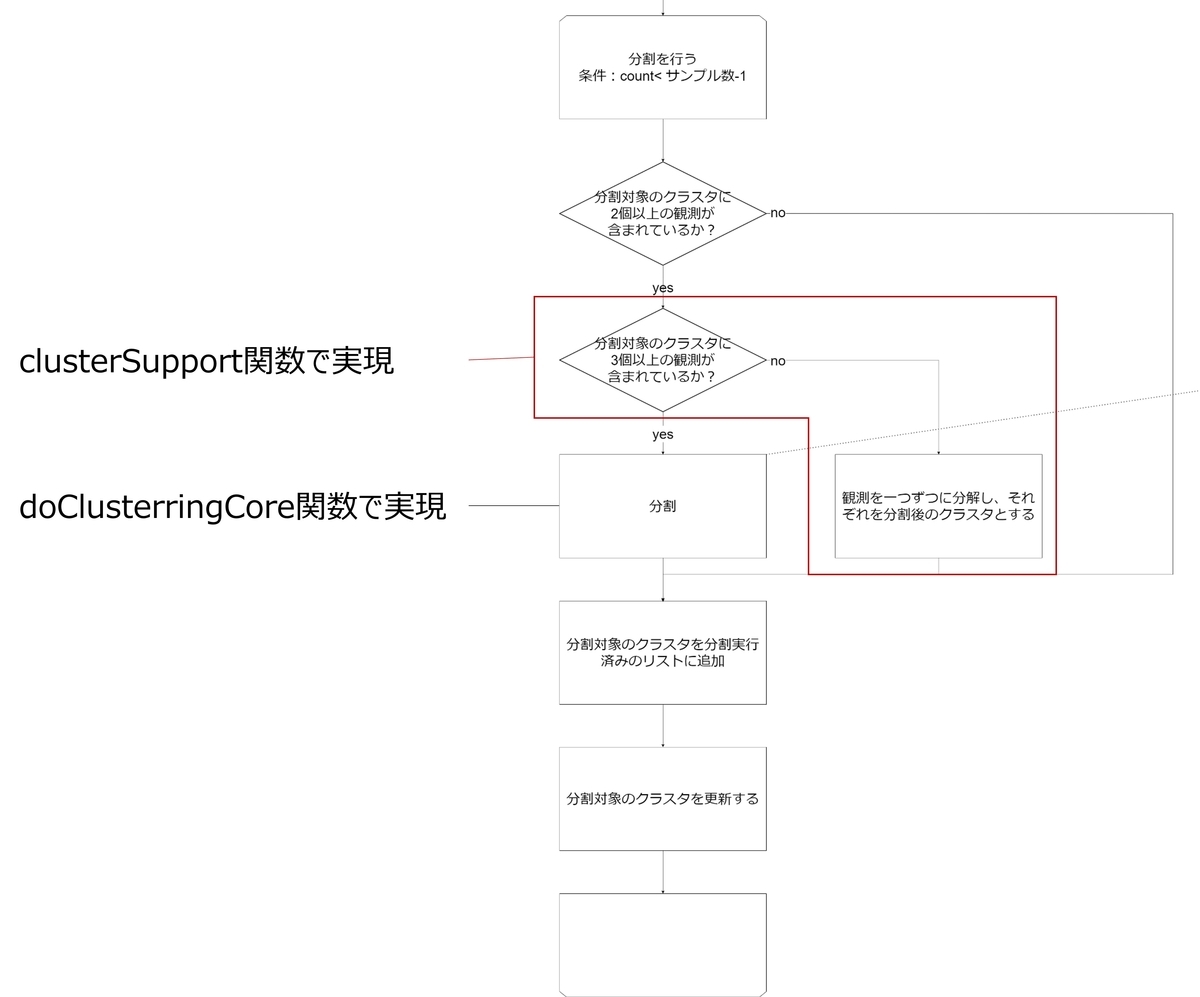
# クラスタに含まれる要素の個数で分割の方法を変える while (count < len(self.df)-1): if len(tmp0_result_DF.iloc[next_clustering]["cluster"]) >= 2: clusterSupoort(rdf = tmp0_result_DF, nc = next_clustering, cd = clustering_done) count += 1 else: clustering_done.append(next_clustering) next_clustering = min([i for i in tmp0_result_DF.index if i not in clustering_done])
アルゴリズム中の「分割」については、doClusteringCore関数で実現していますが、その中身はこちら。
def doClustering(self): # クラスタを分割する関数 def doClusteringCore(target): G1 = target.copy() # 移動元 G2 = [] # 移動先 # 移動すべき1個目の点を決める tmp_d_matrix = self.d_matrix[np.ix_(G1, G1)] maxi = np.argmax( np.apply_along_axis( np.mean, axis = 0, arr = tmp_d_matrix) ) # cluster1のmiをcluster2に移動するメソッド def move(cluster1, cluster2, mi): trans_data = cluster1[mi] cluster1.remove(trans_data) cluster2.append(trans_data) # 点の移動 move(cluster1 = G1, cluster2 = G2, mi = maxi) while True: # 2個目以降の移動すべき点を決める ## G1の各点の他の点との平均距離 tmp_d_matrix = self.d_matrix[np.ix_(G1, G1)] G1_mean = np.apply_along_axis( sum, axis = 0, arr = tmp_d_matrix )/(len(G1)-1) ## G1の各点とG2の各点の平均距離 tmp_d_matrix = self.d_matrix[np.ix_(G1, G2)] d_g1tog2 = np.apply_along_axis( np.mean, axis = 1, arr = tmp_d_matrix ) ## 「G1の各点の他の点との平均距離」-「G1の各点とG2の各点の平均距離」 criterion = G1_mean-d_g1tog2 ## 判定条件の作成 cond = (criterion <= 0) tf = all(cond) # 判定がTrueの場合、while文から抜け出し、分割終了 # 判定がFalseの場合、点を移動させ分割続行 if tf: break else: maxi = np.argmax(criterion) move(cluster1 = G1, cluster2 = G2, mi = maxi) cluster_diff = np.sum(self.d_matrix[np.ix_(G1, G2)])/(len(G1)*len(G2)) # 出力 return([G1, G2, cluster_diff])
最後に出力をdendrogram関数に組み込めるような形に変形します。

# dendrogramに読み込める形に変更する tmp0_result_DF["group_n"] = [len(l) for l in tmp0_result_DF["cluster"]] ## 要素が2個以上のクラスタに対する処理 tmp1_result_DF = ( tmp0_result_DF[tmp0_result_DF["group_n"] >= 2] .sort_values("diff", ascending=False) ) cluster_n = len(self.df) tmp_cluster_no_list = list(range(cluster_n, 2*cluster_n-1)) tmp_cluster_no_list.reverse() tmp1_result_DF["cluster_no"] = tmp_cluster_no_list ## 要素が1個のクラスタに対する処理 tmp2_result_DF = ( tmp0_result_DF[tmp0_result_DF["group_n"] == 1] ) tmp_cluster_no_list = [l[0] for l in tmp2_result_DF["cluster"]] tmp2_result_DF["cluster_no"] = tmp_cluster_no_list ## 要素が2個以上と1個のクラスタに対するresult_DFをunion tmp3_result_DF = ( tmp1_result_DF .append( other = tmp2_result_DF, ignore_index = True ) ) ## childrenから新規に振ったcluster番号を用いてクラスターを表現 cluster_list = [] for c in tmp3_result_DF["children"]: if isinstance(c, list): tmp_series = tmp3_result_DF.loc[tmp3_result_DF["tmp_cluster_no"] == c[0], "cluster_no"] c0 = tmp_series.iloc[-1] tmp_series = tmp3_result_DF.loc[tmp3_result_DF["tmp_cluster_no"] == c[1], "cluster_no"] c1 = tmp_series.iloc[-1] cluster_list.append([c0, c1]) else: cluster_list.append(np.isnan) tmp3_result_DF["cluster_list"] = cluster_list ## 必要なカラムだけ抜き出し、少し処理 tmp_linkage_Z = ( tmp3_result_DF[1<tmp3_result_DF["group_n"]] .sort_values("cluster_no", ascending=True) ) tmp_Z = [] for i in tmp_linkage_Z[["cluster_list", "diff", "group_n"]].itertuples(): i0, i1 = i.cluster_list d = i.diff n = i.group_n tmp_Z.append([i0, i1, d, n]) Z = np.array(tmp_Z)
以上がスクリプト全体です。細切れだと使いにくいと思うので、全体を載せたgitのリンクも貼っておきます。リンク先のIn[6]が該当箇所です。
テスト
簡単なテストデータに対して、作成したスクリプトを動かしてみました。
# テスト用データ作成 test_data = np.array([ [1, 1], [2, 2], [3, 3], [4, 4], [5, 5], [6, 6], [7, 7], [9, 9] ]) # 実行 ## インスタンス作成 test_class = MacnaughtonClustering(df = test_data) ## 距離行列の作成と表示 print(test_class.makeDistanceMatrix()) ## クラスタリング実行 result = test_class.doClustering() ## デンドログラム作成 dendrogram(result)
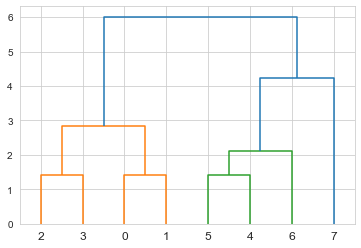
上記のスクリプトで作成したデンドログラムは、図4です。狙った通りのデンドログラムが作成できました。
参考文献
Macnaughton Smith et al. (1965) www.nature.com
カステラ本
