2024-07-26

【深層学習】順序回帰の解説

サイエンス

はじめに

　『深層学習』という下記の本を読んでいます。この本を読んで一発で理解できなかったことをまとめています。本記事では、順序回帰についてまとめていきます。

深層学習　改訂第２版 (機械学習プロフェッショナルシリーズ)

作者:岡谷貴之
講談社

Amazon

順序回帰とは？

　順序回帰問題とは、説明変数 $\boldsymbol{x}$ から順序があるクラス $y$ を当てる問題です。本書では、嗜好品の5段階評価（とても悪い、悪い、普通、良い、とても良い）を予測する問題が挙げられています（図１）。

　順序回帰の特徴は、正解とモデルの予測が異なっていた場合に、「少しだけ外した予測」と「大きく外した予測」が存在することです。先ほどの嗜好品の例でいえば、正解が「とても悪い」の場合に「悪い」と予測することは、「とても良い」と予測するよりはマシと言えます。このように、予測が正解と異なっていた場合でも、その惜しさを考慮することでモデルの精度を高めることが可能と考えられます。
　以上のような特徴を持っている順序回帰を、通常の多クラス分類と同じ方法で解くことは得策と言えません。本記事では、『深層学習』で紹介されている順序回帰を解く方法を2種類紹介します。
　なお、本記事では順序回帰の対象データを次のように設定しておきます。

サンプルサイズ： $N$
$n$ 番目の説明変数： $\boldsymbol{x}_n$
$n$ 番目の目的変数： $y_n$
目的変数のクラス数： $K$

　また、モデルは深層学習モデルを想定しています。

順序回帰を解く方法

二値分類に変換する方法

　一つ目の方法は、順序回帰を二値分類に変換する方法です。順序回帰を次のようにして解きます。

目的変数の変換
目的変数 $y_n = \bar{k}$ を

$d_{nk} = \left\{ \begin{array}{ll} 1 & (k<\bar{k}) \\ 0 & ({\rm otherwise}) \end{array} \right.$

に変換して、目的変数を $\boldsymbol{d} _ n = (d _ {n1}, \cdots, d _ {nK-1})$ とします。

モデル
　深層学習モデルの出力層に $K-1$ 個のユニットを並べ、ロジスティック関数による変換を行い予測とします（図２）。

損失関数
損失関数として、交差エントロピーを用います。なお、交差エントロピーとはモデルに含まれるパラメータを $\boldsymbol{w}$ 、予測を $\hat{\boldsymbol{d}_n} = (\hat{d} _ {n1}, \cdots, \hat{d} _ {nK-1}) \in [0, 1]^{K-1}$ としたときに、

$E(\boldsymbol{w}) = - \displaystyle{\sum_{n=1}^{N}}\displaystyle{\sum_{k=1}^{K-1}} {\rm log} \hat{d}_{nk}(\boldsymbol{x_n}; \boldsymbol{w})^{d_{nk}}$

と表現される式です。

予測の出し方
次の式で予測を出します。

$\hat{y}_n = 1+ \displaystyle{\sum_{k=1}^{K-1}}\boldsymbol{1}(\hat{d}_{nk})$

なお、 $\boldsymbol{1}(\hat{d} _ {nk})$ は何らかの方法で $\hat{d} _ {nk}$ を $0$ か $1$ に変換する関数です。例えば、適当な閾値 $\gamma_k$ を用いて

$\boldsymbol{1}(\hat{d}_{nk}) = \left\{ \begin{array}{ll} 1 & (\hat{d}_{nk} \geq \gamma_k) \\ 0 & (\hat{d}_{nk} < \gamma_k) \end{array} \right.$

とする関数が考えられます。
　また、この予測 $\hat{y}_n$ はある条件下で一次平均収束する予測であることが示せます。つまり、

$\displaystyle{\lim_{N \to +\infty}} E\left[|\hat{y}_n-\bar{k}| \middle| \boldsymbol{x} \right] = 0$

が成り立ちます。このことの証明は、別記事で書こうと思います。

目的変数をソフトラベルに変換する方法

　二つ目の方法は、one-hot-encodingされている目的変数をソフトラベルに変換する方法です。順序回帰を次のようにして解きます。

目的変数の変換
目的変数 $y_n = \bar{k}$ を

$d_{nk} = \dfrac{{\rm exp}(-|\bar{k}-k|)}{{\displaystyle{\sum_{k=1}^{K}}\rm exp}(-|\bar{k}-k|)}$

に変換して、目的変数を $\boldsymbol{d} _ n = (d _ {n1}, \cdots, d _ {nK})$ とします。なお、このように定義されるラベルはソフトラベルと呼ばれます。

モデル
　深層学習モデルの出力層に $K$ 個のユニットを並べ、ソフトマックス関数による変換を行い予測とします（図３）。

損失関数
損失関数として、交差エントロピーを用います。
予測の出し方
次の式で予測を出します。

$\hat{y}_n = \underset{k}{{\rm argmax}}\{\hat{d}_{nk}\}$

　また、この予測 $\hat{y}_n$ はある条件下で一次平均収束する予測であることが示せます。このことの証明も、一つ目の方法と同様に別記事で書こうと思います。

まとめ

　本記事では、『深層学習』に記載の順序回帰を解く方法をまとめました。どちらの方法も目的変数を変換すること、その目的変数に合わせたモデルを構築することが必要だと学びました。

2024-07-16

【PyTorch】畳み込み演算の次元数変化：チュートリアルの解説

エンジニアリングサイエンス

はじめに

　PyTorchのチュートリアル PyTorch60分講座: ニューラルネットワーク入門を勉強しました。本記事では、チュートリアル記載のLeNetがどのように入力画像の次元数を変化させていくのかについてまとめようと思います。
　なお、私もチュートリアルを読んでいる際に混乱したのですが、チュートリアルに記載のLeNetの構造を表した図と、チュートリアル中に書かれているコード（Netクラス）は若干構造が異なっています（図１）。本記事では、コードを正として説明します。

畳み込み演算による次元数の変化

　本節では、畳み込み演算による入力画像の次元数の変化について説明します。下記のような設定とします。

入力画像
- チャネル数： $C _ {\rm in}$
- 縦幅： $H _ {\rm in}$
- 横幅： $W _ {\rm in}$
フィルタ
- 縦幅： $H _ F$
- 横幅： $W _ F$
ストライド： $S$
出力画像
- チャネル数： $C _ {\rm out}$

　このとき、畳み込み演算では次の手順にしたがって計算が行われます。

まず、 $C _ {\rm in}$ 個のフィルタが用意され、入力画像との積和をとる
次に、1で計算された出力の画素を全チャネルにわたって和をとる
上記の作業を $C _ {\rm out}$ 回行うことで、出力画像のチャネル数を $C _ {\rm out}$ にする

　図２は上記の作業をまとめたものです。

　以上より、次元数が $({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = (C _ {\rm in}, H _ {\rm in}, W _ {\rm in})$ の入力画像が畳み込み演算によって、 $({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = \left(C _ {\rm out}, \left\lfloor \frac{ H _ {\rm in}-H _ F}{S} \right\rfloor+1, \left\lfloor \frac{W _ {\rm in}-W _ F}{S}\right\rfloor+1 \right)$ に変化します。ただし、 $\lfloor \cdot \rfloor$ は小数点以下を切り捨てて、整数に変換する関数です。

プーリングによる次元数の変化

　本節では、プーリングによる入力画像の次元数の変化について説明します。とはいえ、畳み込み演算とほとんど同じです。下記のような設定とします。

入力画像
- チャネル数： $C _ {\rm in}$
- 縦幅： $H _ {\rm in}$
- 横幅： $W _ {\rm in}$
ウィンドウサイズ
- 縦幅： $H _ W$
- 横幅： $W _ W$
ストライド： $S$
出力画像
- チャネル数：プーリングではチャネル数が変化しないので、 $C _ {\rm in}$ のまま

　図3はプーリングの計算手順をまとめたものです。

　以上より、次元数が $({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = (C _ {\rm in}, H _ {\rm in}, W _ {\rm in})$ の入力画像がプーリングによって、 $({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = \left(C _ {\rm in}, \left\lfloor \frac{ H _ {\rm in}-H _ W}{S} \right\rfloor+1, \left\lfloor \frac{W _ {\rm in}-W _ W}{S}\right\rfloor+1 \right)$ に変化します。

LeNetによる次元数の変化

　以上を踏まえて、LeNetが32×32の入力画像の次元数をどのように変化させるのかについて説明します。まず、LeNetの構造を改めて文字で書き起こします。

$C _ {\rm in} = 1, C _ {\rm out} = 6, H _ F = W _ F = 3, S = 1$ の畳み込み演算を行う
$C _ {\rm in} = 1, H _ W = W _ W = 2, S = 2$ の最大値プーリングを行う
$C _ {\rm in} = 6, C _ {\rm out} = 16, H _ F = W _ F = 3, S = 1$ の畳み込み演算を行う
$C _ {\rm in} = 16, H _ W = W _ W = 2, S = 2$ の最大値プーリングを行う
576次元のベクトルに変換する
576次元から120次元への線形変換を行う
120次元から84次元への線形変換を行う
84次元から10次元への線形変換を行う

　以上の変換のうち、5～8は単純な線形変換です。したがって、次元数の変化は上記に書いてある通りなので説明しません。1～4の変換について次元数がどのように変化するのか説明します。

1の変換

　畳み込み演算によって計算された出力画像の次元数は、 $({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = \left(C _ {\rm out}, \left\lfloor \frac{ H _ {\rm in}-H _ F}{S} \right\rfloor+1, \left\lfloor \frac{W _ {\rm in}-W _ F}{S}\right\rfloor+1 \right)$ でした。これに、 $C _ {\rm out} = 6, H _ {\rm in} = W _ {\rm in} = 32, H _ F = W _ F = 3, S = 1$ を代入することで、

$({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = (6, 30, 30)$

となります。

2の変換

　プーリングによって計算された出力画像の次元数は、 $({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = \left(C _ {\rm in}, \left\lfloor \frac{ H _ {\rm in}-H _ W}{S} \right\rfloor+1, \left\lfloor \frac{W _ {\rm in}-W _ W}{S}\right\rfloor+1 \right)$ でした。これに、 $C _ {\rm in} = 6, H _ {\rm in} = W _ {\rm in} = 30, H _ W = W _ W = 2, S = 2$ を代入することで、

$({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = (6, 15, 15)$

となります。

3の変換

　 $C _ {\rm out} = 16, H _ {\rm in} = W _ {\rm in} = 15, H _ F = W _ F = 3, S = 1$ なので、1の変換と同様に計算すると

$({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = (16, 13, 13)$

となります。

4の変換

　 $C _ {\rm in} = 16, H _ {\rm in} = W _ {\rm in} = 13, H _ W = W _ W = 2, S = 2$ なので、2の変換と同様に計算すると

$({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = (16, 6, 6)$

となります。

以上より、1～4の変換によって32x32の画像が16x6x6=576次元のベクトルに変換できました。

LeNetに入力できる画像の範囲

　ここからはおまけです。
　畳み込み演算やプーリングによる出力画像の次元数の計算には、床関数（ $\lfloor \cdot \rfloor$ ）が含まれていました。したがって、入力画像のサイズが32x32と多少異なっていてもうまいこと床関数が次元数を調整し、576次元の全結合層に入力できるベクトルを得られる可能性があります。本節では、「入力画像のサイズを32x32からどれくらい変えてもLeNetに入力できるのか？」ということを考えようと思います。ただし、簡単のため入力画像は正方形とします。

　まず、LeNetの入力画像の縦幅を $H$ とします。このとき、入力画像は正方形であることを仮定しているので横幅も $H$ となります。この入力画像に1の畳み込み演算による変換を行うと、出力画像のサイズは、

$\begin{eqnarray} ({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) &=& \left(6, \left\lfloor H-3 \right\rfloor+1, \left\lfloor H-3 \right\rfloor+1 \right) \\ &=& (6, H-2, H-2) \end{eqnarray}$

となります。ただし、 $H \in \mathbb{N}$ なので $H-2 \in \mathbb{N}$ となることを利用しました。
　同様に2のプーリングによる変換を行うと、出力画像のサイズは、

$\begin{eqnarray} ({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) &=& \left(6, \left\lfloor \dfrac{(H-2)-2}{2} \right\rfloor+1, \left\lfloor \dfrac{(H-2)-2}{2} \right\rfloor+1 \right) \\ &=& \left(6, \left\lfloor \dfrac{H}{2}\right\rfloor-1, \left\lfloor \dfrac{H}{2}\right\rfloor-1 \right) \end{eqnarray}$

となります。ここで、 $H _ 1 = \left \lfloor \dfrac{H}{2} \right \rfloor-1$ としておきます。
　同様の計算方法で、3の畳み込み演算を行うと、出力画像のサイズは、

$\begin{eqnarray} ({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = = (16, H_1-2, H_1-2) \end{eqnarray}$

となります。また、4のプーリング演算を行うと、最終的な出力画像のサイズは、

$\begin{eqnarray} ({\rm チャネル数}, {\rm 縦幅}, {\rm 横幅}) = = \left(16, \left\lfloor \dfrac{H_1}{2}\right\rfloor-1, \left\lfloor \dfrac{H_1}{2}\right\rfloor-1 \right) \end{eqnarray}$

となります。
　このとき、上記の出力画像を576次元ベクトルに変換し全結合層に入力するので、

$\begin{eqnarray} 16 \times \left(\left\lfloor \dfrac{H_1}{2}\right\rfloor-1\right) \times \left( \left\lfloor \dfrac{H_1}{2}\right\rfloor-1 \right) = 576 \end{eqnarray}$

となります。これより、

$\begin{eqnarray} \left\lfloor \dfrac{H_1}{2}\right\rfloor-1 = 6 \end{eqnarray}$

となります。
　一般的に、任意の $x \in \mathbb{R}, k \in \mathbb{N}$ に対して、 $\lfloor x \rfloor = k \Leftrightarrow k \leq x \lt k+1$ が成り立ちます。これを用いると、 $\left\lfloor \dfrac{H_1}{2}\right\rfloor-1 = 6$ から、 $14 \leq H _ 1 \lt 16$ となります。
　次に $H _ 1 = \left \lfloor \dfrac{H}{2} \right \rfloor-1$ を使うと、 $15 \leq \left\lfloor \dfrac{H}{2} \right\rfloor \lt 17$ となり、ここから

$\begin{eqnarray} 30 \leq H < 34 \end{eqnarray}$

となります。
　以上のことから、LeNetに入力可能な画像のサイズは正方形の場合、30×30、31×31、32×32、33×33の4パターンに限られることがわかります。実際に、入力画像のサイズを変えて実行してみると、図４のような結果になりました。

　コードにおいても入力画像が4パターンしかないことを示せました。

まとめ

　本記事では、LeNetを題材に畳み込み演算とプーリングによって次元数がどのように変わるのかについて説明しました。また、LeNetに入力できる画像の範囲についても考察しました。

2024-06-25

【Python】浅いコピー・深いコピーを図解する

エンジニアリング

はじめに

　Pythonの浅いコピーと深いコピーについて勉強したのでまとめようと思います。

浅いコピー・深いコピーの定義

　Pythonの公式ドキュメントでは、浅いコピーと深いコピーを下記のように定義しています。

浅い (shallow) コピーと深い (deep) コピーの違いが関係するのは、複合オブジェクト (リストやクラスインスタンスのような他のオブジェクトを含むオブジェクト) だけです:
・浅いコピー (shallow copy) は新たな複合オブジェクトを作成し、その後 (可能な限り) 元のオブジェクト中に見つかったオブジェクトに対する参照を挿入します。
・深いコピー (deep copy) は新たな複合オブジェクトを作成し、その後元のオブジェクト中に見つかったオブジェクトのコピーを挿入します。

　本記事では、この定義の意味をかみ砕いて説明しようと思います。

複合オブジェクト

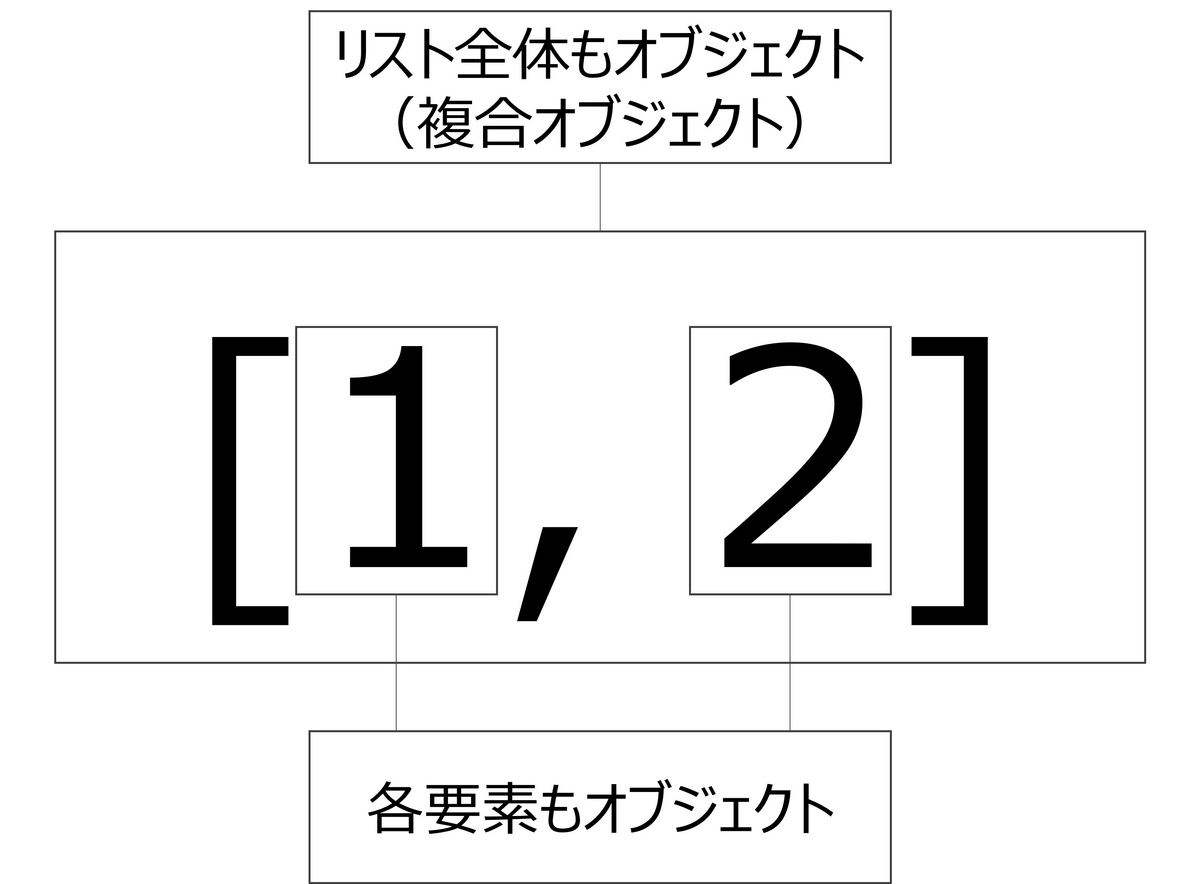
　浅いコピーと深いコピーの定義に「浅い (shallow) コピーと深い (deep) コピーの違いが関係するのは、複合オブジェクト (リストやクラスインスタンスのような他のオブジェクトを含むオブジェクト) だけです」と記載があります。本節では、複合オブジェクトの意味を説明します。
　Pythonでは、Pythonが扱うデータやプログラムコードは全てオブジェクトと呼ばれます。また、オブジェクトを複数集めて構成されるオブジェクトは複合オブジェクトと呼ばれます。
　複合オブジェクトの例として、リストがあります。リストは、[1, 2]などで定義されるオブジェクトですが、その要素1, 2もそれぞれオブジェクトです（図１）。したがって、オブジェクト[1, 2]はオブジェクト1とオブジェクト2を集めて構成される複合オブジェクトということができます。
　浅いコピーと深いコピーはこの複合オブジェクトに関する話題です。　

オブジェクトの作成

　浅いコピーと深いコピーの定義に両方とも「新たな複合オブジェクトを作成し」との記述があります。本節では、この記述の意味について、コードを通して説明します。
　まずは、下記のコードをご覧ください。

import copy

l = [[0, 1], [2, 3]]

# 浅いコピーでもなく、深いコピーでもない
l_copy = l

# 浅いコピー
l_shallowcopy = l.copy()

# 深いコピー
l_deepcopy = copy.deepcopy(l)

# オブジェクトIDの表示
print(f"id(l)            ={id(l)}")
print(f"id(l_copy)       ={id(l_copy)}")
print(f"id(l_shallowcopy)={id(l_shallowcopy)}")
print(f"id(l_deepcopy)   ={id(l_deepcopy)}")

　出力結果は下表のようになりました。

変数名	オブジェクトID
l	140418773848128
l_copy	140418773848128
l_shallowcopy	140418773850368
l_deepcopy	140418773848704

　オブジェクトIDとは、Pythonの全てのオブジェクトに振られている固有の番号です。したがって、次のことがいえます。

l_copyとlはオブジェクトIDが同じ→l_copyとlは同じオブジェクト
l_shallowcopyとlはオブジェクトIDが異なる→l_shallowcopyとlは異なるオブジェクト
l_deepcopyとlはオブジェクトIDが異なる→l_deepcopyとlは異なるオブジェクト

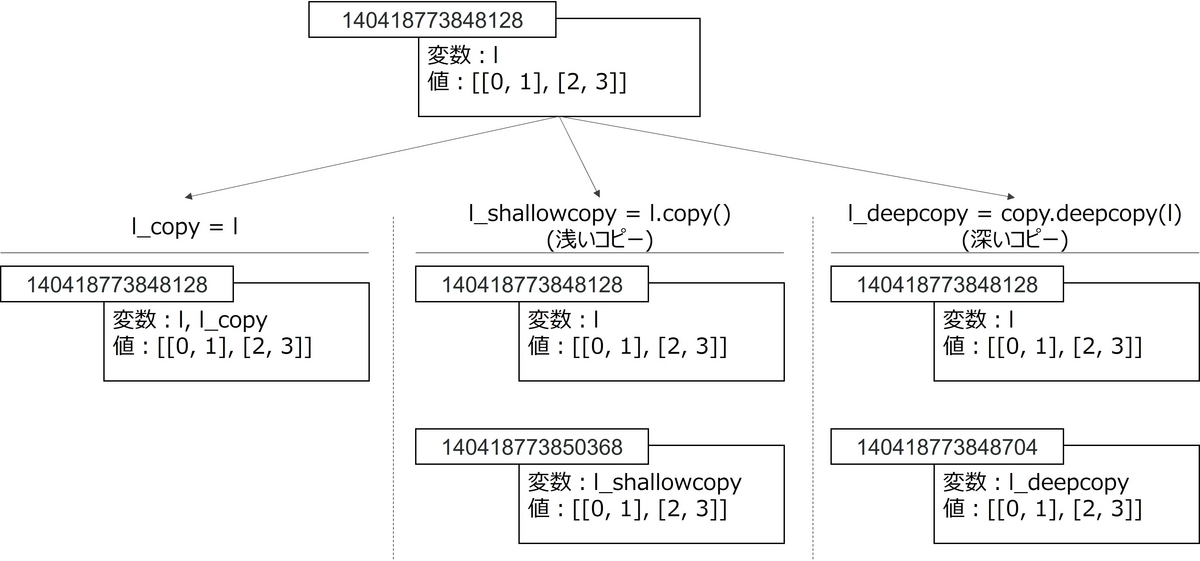
　以上より、l_copy = lでは新しいオブジェクトを作成しませんが、浅いコピー・深いコピーでは新しいオブジェクトを作成していることがわかります。図２はこれをまとめた図です。

元のオブジェクト中に見つかったオブジェクトに対する参照

　浅いコピーの定義には、「元のオブジェクト中に見つかったオブジェクトに対する参照を挿入します」と書かれています。これについて説明します。
　まずは、下記のコードをご覧ください。

for i in range(0, len(l)):
  print(f"id(l[{i}]) = {id(l[i])}, id(l_shallowcopy[{i}]) = {id(l_shallowcopy[i])}")

　出力結果は下記のようになりました。

変数名	オブジェクトID
l [0]	140419284311104
l_shallowcopy[0]	140419284311104
l [1]	140418773763520
l_shallowcopy[1]	140418773763520

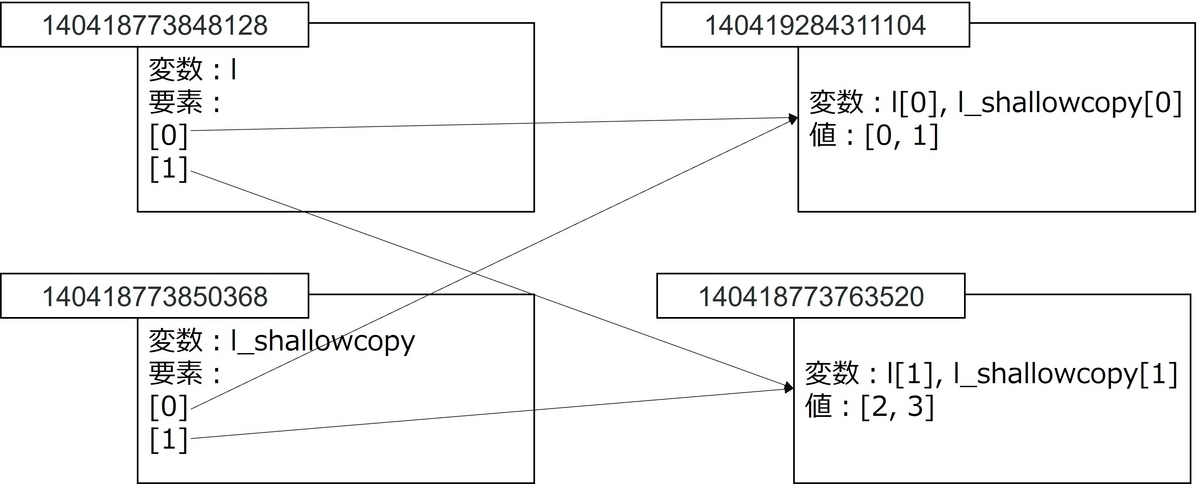
　上表を見ると、l[0]とl_shallowcopy[0]のオブジェクトが、l[1]とl_shallowcopy[1]のオブジェクトが一致していることがわかります。つまり、浅いコピーを行うと、新規の複合オブジェクトが作成されるが、その要素については新しいオブジェクトが作成されません。
　これが、「元のオブジェクト中に見つかったオブジェクトに対する参照を挿入します」の意味です。図３はこのことを説明した図です。

元のオブジェクト中に見つかったオブジェクトのコピーを挿入

　深いコピーの定義には、「元のオブジェクト中に見つかったオブジェクトのコピーを挿入」と書かれています。これについて説明します。
　浅いコピーと同様な下記のコードをご覧ください。

for i in range(0, len(l)):
  print(f"id(l[{i}]) = {id(l[i])}, id(l_deepcopy[{i}]) = {id(l_deepcopy[i])}")

　出力結果は下記のようになりました。

変数名	オブジェクトID
l [0]	140419284311104
l_deepcopy[0]	140418773849152
l [1]	140418773763520
l_deepcopy[1]	140418773849856

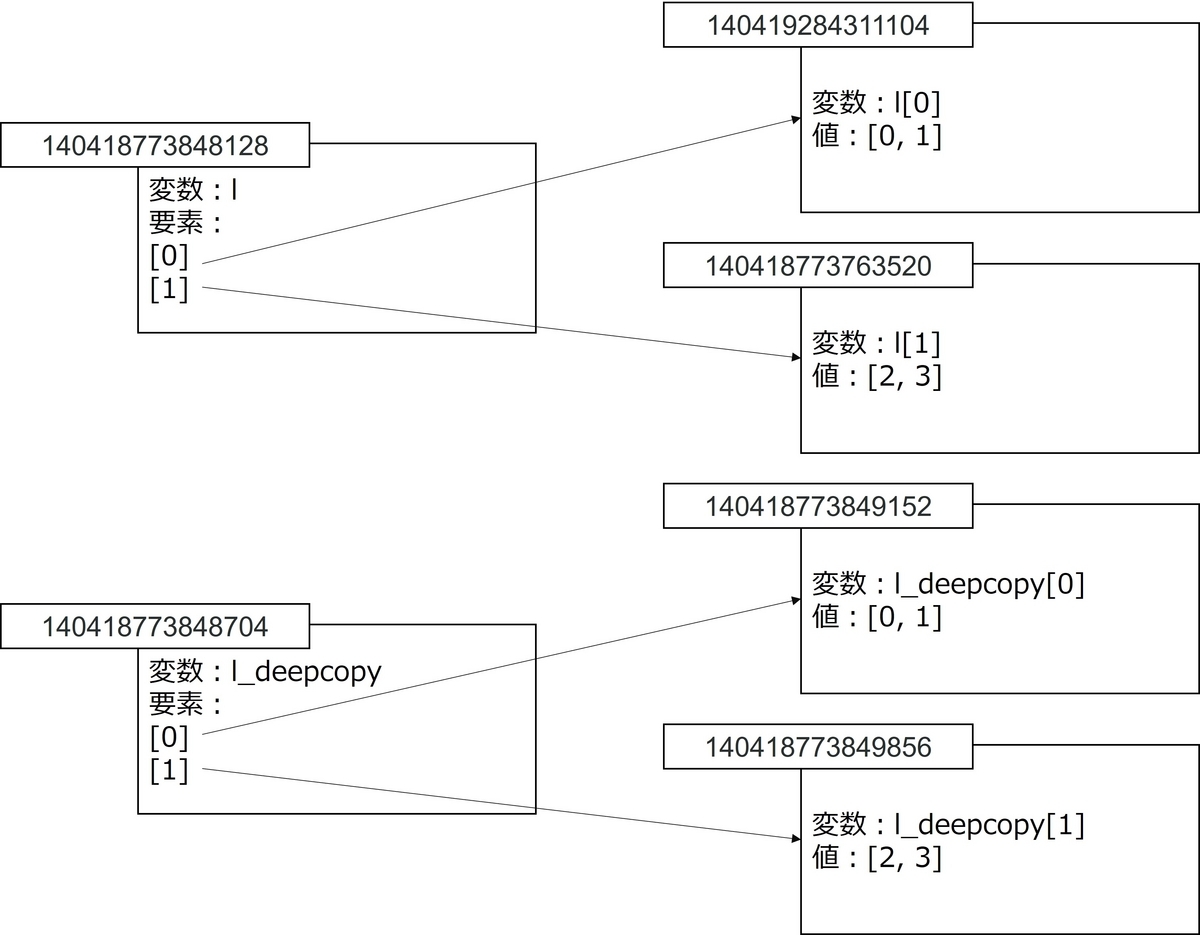
　上表を見ると、l[0]とl_deepcopy[0]のオブジェクト、l[1]とl_deepcopy[1]のオブジェクトが異なることがわかります。つまり、深いコピーを行うと、新規のオブジェクトが作成され、さらにその要素についても新しいオブジェクトが作成されます。
　これが、「元のオブジェクト中に見つかったオブジェクトのコピーを挿入」の意味です。図４はこのことを説明した図です。

要素の値を変更したらどうなる？

ミュータブルな要素の値を変更したとき

　本節では、元の複合オブジェクトの要素を変更したときに、浅いコピーと深いコピーで作成されたオブジェクトの挙動を説明します。ただし、元の複合オブジェクトの要素はミュータブルとします。
　まずは、次のコードをご覧ください。

l[0][0] = 100

print(f"l = {l}")
print(f"l_shallowcopy = {l_shallowcopy}")
print(f"l_deepcopy = {l_deepcopy}")

　出力結果は下記のようになりました。

変数名	値
l	[[100, 1], [2, 3]]
l_shallowcopy	[[100, 1], [2, 3]]
l_deepcopy	[[0, 1], [2, 3]]

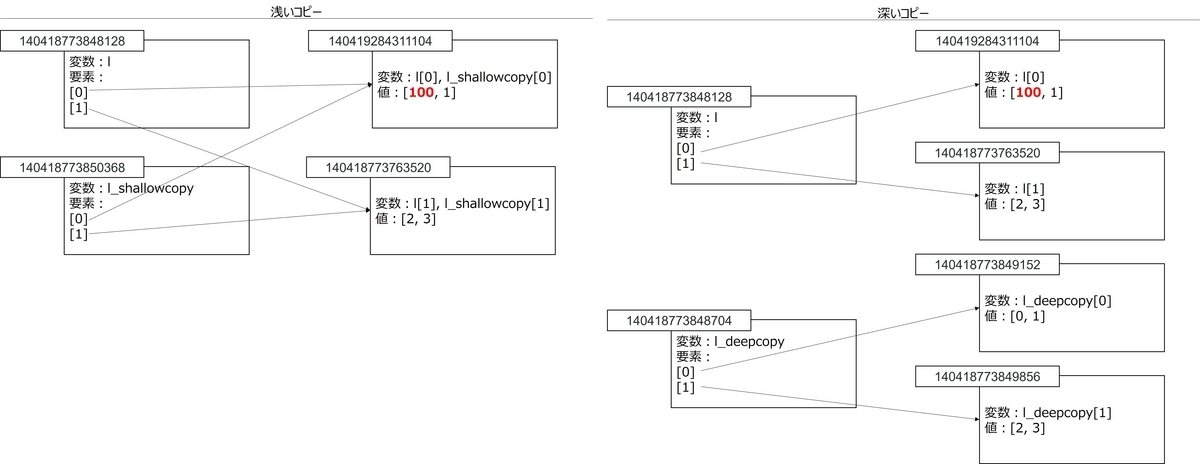
　l_shallowcopyはlの変更に伴い値が変更されました。これは、l_shallowcopy[0]とl[0]のオブジェクトが一致しているためです。
　一方、l_deepcopyはlの変更に伴った値の変更がありません。これは、l_deepcopy[0]とl[0]のオブジェクトが一致していないためです。図５はこのことを説明した図です。

　なお、上記のような挙動となるのは複合オブジェクトの要素がミュータブルなときであることに注意してください。l[0]のオブジェクトはリストなので、ミュータブルです。したがって、l[0][0]の値が変更されても、l[0]のオブジェクト自体は変わらず、l_shallowcopy[0]の値も変更されました。

イミュータブルな要素の値を変更したとき

　最後に元の複合オブジェクトの要素を変更したときに、浅いコピーと深いコピーで作成されたオブジェクトの挙動を説明します。ただし、元の複合オブジェクトの要素はイミュータブルとします。
　まずは、次のコードをご覧ください。

import copy

l = [0, 1]

# 浅いコピー
l_shallowcopy = l.copy()

# 深いコピー
l_deepcopy = copy.deepcopy(l)

# lの要素を変更
l[0] = 100

# 表示
print(f"l = {l}")
print(f"l_shallowcopy = {l_shallowcopy}")
print(f"l_deepcopy = {l_deepcopy}")

　出力結果は下記のようになりました。

変数名	値
l	[100, 1]
l_shallowcopy	[0, 1]
l_deepcopy	[0, 1]

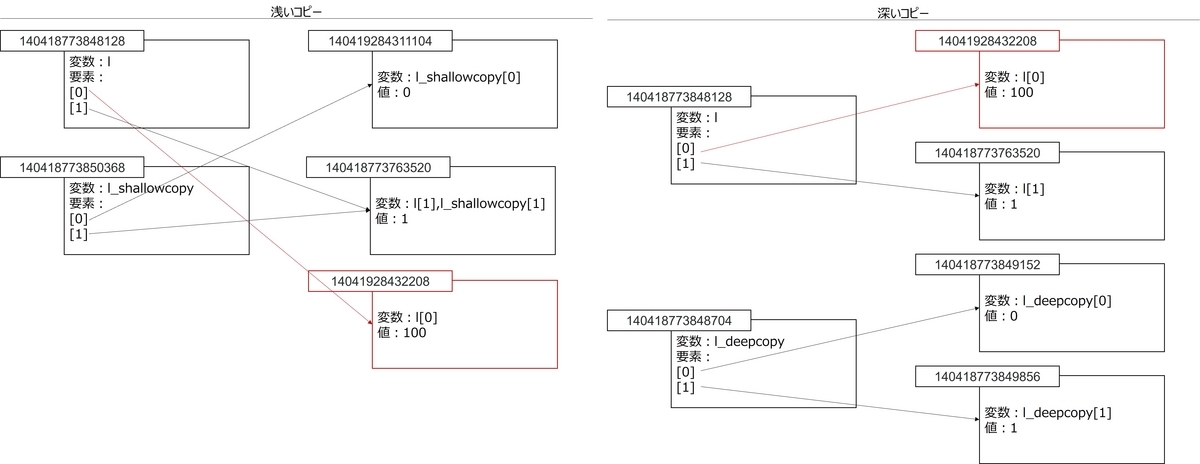
　上表を見ると、l[0]の変更に伴ったl_shallowcopy[0]の変更がありません。l = [[0, 1], [2, 3]]のときは、l_shallowcopyの値が変更されたのに、今回は値が変更されていません。なぜでしょうか？
　その答えは、l[0]がイミュータブルなオブジェクトだからです。イミュータブルなオブジェクトの場合、値を変更すると新しいオブジェクトが作成されます。したがって、l[0]は新しいオブジェクトになるが、l_shallowcopy[0]は元のオブジェクトを参照しているため、値が異なるという結果になります。図６はこのことを説明した図です。

まとめ

本記事では、Pythonにおける浅いコピーと深いコピーについて説明しました。浅いコピーと深いコピーの特徴は次のようにまとめられます。

浅いコピー
- 浅いコピーをすると、新しい複合オブジェクトが作成される。しかし、その要素は元のオブジェクトと同じ。
- 元の複合オブジェクトの要素を変更すると
  - 要素がミュータブルな場合、浅いコピーによって作成された複合オブジェクトの要素も変更される。
  - 要素がイミュータブルな場合、浅いコピーによって作成された複合オブジェクトの要素は変更されない。
深いコピー
- 深いコピーをすると、新しい複合オブジェクトが作成される。また、その要素も新しいオブジェクトになる。
- 元の複合オブジェクトの要素を変更すると
  - 要素がミュータブル、イミュータブルに関係なく、深いコピーによって作成された複合オブジェクトの要素は変更されない。

2024-06-23

【PyTorch】テンソルがraw majorであることの確認

エンジニアリング

はじめに

　↓の過去記事で「PyTorchでは、テンソルが作成されたとき、その要素はメモリ上にraw majorと呼ばれる方式で並びます」と書きました。本記事では、テンソルの要素がraw majorで並んでいることを、各要素のメモリアドレスを見ることで確認します。

aisinkakura-datascientist.hatenablog.com

raw majorとは？

　raw majorとは行列を図１の上図に記載した順番でメモリに乗せることをいいます。また、raw majorと対応する言葉として、column majorがあります。column majorは図１の下図に記載した順番でメモリに乗せることをいいます。

PyTorchのテンソルがraw majorで並んでいることの確認

　テンソルが格納されているメモリの先頭アドレスは、data_ptr()メソッドを使うことで取得できます。なので、下記のコードで全ての要素の先頭メモリアドレスを表示させることができます。

import itertools
import torch

x = torch.tensor([[1, 2, 3], [4, 5, 6]])
for i, j in itertools.product(range(x.size(0)), range(x.size(1))):
  print(f"x[{i}, {j}] address: {x[i, j].data_ptr()}")

　私の環境では、結果は図２のようになりました。

　したがって、今回定義したテンソルxの各要素は図３のようにメモリ上に乗っています。

　以上より、PyTorchのテンソルがraw majorで並んでいることを確認できました。

2024-06-19

【PyTorch】viewとreshapeの違い

エンジニアリング

はじめに

　PyTorchには、テンソルを変形するメソッドとしてtorch.Tensor.viewとtorch.Tensor.reshapeが用意されています。本記事では、メソッドviewとreshapeの違いについてまとめます。

本記事のサマリ

viewは要素が順に並んでいるときしか使えない。reshapeは、要素が順に並んでいないときでも、テンソルを変形できる
テンソルの要素がメモリ上で順に並んでいるとは、テンソルの要素が連続したメモリに配置されているということ
テンソルを転置すると、テンソルの要素がメモリ上で順に並んだ状態ではなくなり、viewを使えなくなる

`view`と`reshape`の違い

　viewとreshapeの違いを図１にまとめました。viewは要素が順に並んでいるときしか使えないです。reshapeは、要素が順に並んでいないときでも、テンソルを変形できます。

　なお、要素が順に並んでいないときでも、メソッドcontiguousを使って要素を順に並び替えることができます。その後viewを適用すれば、エラーは出力されません。その場合、下記のようにして使います。

import torch

# テンソルを作成
x = torch.tensor([[1, 2, 3], [4, 5, 6]])

# 転置（このときに、テンソルの要素が順に並んでいない状態になる）
y = torch.t(x)

# viewを適用するとRuntimeErrorを出力する
y_view = y.view(2, 3)
# -> RuntimeError: view size is not compatible with input tensor's size and stride (at least one dimension spans across two contiguous subspaces). Use .reshape(...) instead.

# contiguousを適用してから、viewを適用するとRuntimeErrorは出力されない
y_view = y.contiguous().view(2, 3)

テンソルの要素がメモリ上の順に並んでいるとは？

　ここまで、「テンソルの要素がメモリ上の順に並んでいる」と書いてきました。これがどういう意味を持つのか、もう少し詳しく説明します。
　PyTorchでは、テンソルが作成されたとき、その要素はメモリ上にraw majorと呼ばれる方式で並びます。例えば、2×3のテンソルxを作成したとき、その要素はメモリ上に図２のように並びます。

　この状態を「テンソルの要素がメモリ上の順に並んでいる」と呼んでいます。

テンソルを呼び出すときの挙動

　テンソルが呼び出されたとき、内部では下記の挙動をしています。

x[0, 0]の値をメモリから取り出す
strideに基づいて、各要素の値をメモリから取り出す

　01において、「x[0, 0]の値をメモリから取り出す」と書きました。これは、テンソルxにx[0, 0]のメモリ番号が記録されており、その情報を基に値を取り出せます。なお、x[0, 0]のメモリ番号は次のコードで確認できます。

print(x.data_ptr())

# または
print(x[0, 0].data_ptr())

　次に、02の説明をします。
　x[0, 0]より後の要素を取り出すときは、テンソルに記録されているstrideというものを使います。strideとは、各次元において添え字を1つ増やすときに何個隣のメモリを見れば良いのか、を表す指標です。例えば、xの場合、strideは(3, 1)と記録されています。これは、0次元目の添え字を1つ増やすときは3個隣のメモリを、1次元目の添え字を1つ増やすときは1個隣のメモリを見よという意味です。つまり、x[1, 0]を取り出すには、x[0, 0]の3個隣のメモリを見ることで取り出し、x[0, 1]を取り出すには、x[0, 0]の1個隣のメモリを見ることで取り出します（図３）。

　なお、テンソルのstrideは下記のコードで確認できます。

print(x.stride())

テンソルを転置すると何が起きるか？

　テンソルを転置すると、何が起きるか見ていきます。
　PyTorchにおいては、テンソルを転置しても新しくメモリ上に要素が配置されるわけではありません。strideの値が変わるだけです。今回の場合、xを転置したyのstrideは、xのstrideをひっくり返した(1, 3)となります。したがって、yについて下記のことがいえます。

y[0, 0]のメモリ番号はx[0, 0]と同じ
y[i+1, j]を取り出すときには、y[i, j]の1個隣を見る
y[i, j+1]を取り出すときには、y[i, j]の3個隣を見る

　具体的には、図４のようになります。

　このとき、メモリ上でyの要素は図５のように並び、raw majorになっていません。したがって、「テンソルの要素がメモリ上の順に並んでいない」状態となり、viewを使うことができなくなります。

まとめ

viewは要素が順に並んでいるときしか使えない。reshapeは、要素が順に並んでいないときでも、テンソルを変形できる
テンソルの要素がメモリ上で順に並んでいるとは、テンソルの要素が連続したメモリに配置されているということ
テンソルを転置すると、テンソルの要素がメモリ上で順に並んだ状態ではなくなり、viewを使えなくなる

参考文献

2024-06-17

【PyTorch】モデルの保存と読み込み

エンジニアリング

はじめに

　PyTorchのチュートリアルを勉強しています。本記事では「0. PyTorch入門」の「 7. モデルの保存・読み込み」を学んだ結果をまとめようと思います。

モデルの保存・読み込み方法

　PyTorchで作成したモデルの保存・読み込み方法を図１にまとめました。

　具体的なコードは下記です。

モデルの重みだけを保存する

　下記のようにして、モデルの重みを保存します。なお、ファイルの拡張子は.pthが使われることが多いようです。

import torch
from torchvision import models

# 画像認識モデルVGG16の訓練済みモデルを読み込む（例）
model = models.vgg16(pretrained=True)

# モデルの重みのみを保存する
torch.save(model.state_dict(), 保存先のパス)

　読み込む際は、先にモデルのインスタンスを作成しておき、そこに保存された重みを設定します。

import torch
from torchvision import models

# モデルのインスタンスを作成
model = models.vgg16()

# モデルの重みの読み込み
model_weights = torch.load(モデルのパス)

# モデルの重みをモデルのインスタンスに設定
model.load_state_dict(model_weights)

モデルの重みだけでなく構成も保存するーPyTorchでしか読み込めない方法

　下記のようにして、モデルの重みや構成を保存します。こちらも、ファイルの拡張子は.pthが使われることが多いようです。

import torch

# モデル全体の保存
torch.save(model, 保存先のパス)

　下記のコードで読み込みます。

import torch
# モデル全体を読み込む
model = torch.load(モデルのパス)

モデルの重みだけでなく構成も保存するーPyTorch以外でも読み込める方法

　図１中のNo.1とNo.2の保存方法は、PyTorchでモデルを読み込み、推論することができます。しかし、No.3の保存方法では、PyTorchでモデルを読み込み、推論することができません。
　本節ではNo.3で保存されたモデルの読み込みと推論の仕方について説明します。
　まず、onnx形式で保存されたモデルを読み込み、モデルに問題ないこととモデルの構造を確認します。

import onnx

# onnx形式で保存されたモデルの読み込み
model = onnx.load(モデルのパス)

# モデルに問題ないことの確認
onnx.checker.check_model(model)

# モデルの構造の表示
print(onnx.helper.printable_graph(model.graph))

　モデルの構造は下記のように表示されました。

graph main_graph (
  %input.1[FLOAT, 1x3x224x224]
) initializers (
  %features.0.weight[FLOAT, 64x3x3x3]
  %features.0.bias[FLOAT, 64]
~(略)~

　次に推論を実行します。下記のコードで実行します。

import numpy as np
import onnxruntime

# 実行セクションを作成
sess = onnxruntime.InferenceSession(
    モデルのパス,
    providers=["CUDAExecutionProvider", "CPUExecutionProvider"]
)

# データ作成
rng = np.random.default_rng()
input_image = rng.random((1, 3, 224, 224)).astype(np.float32) # 上記でグラフの構造を表示したときのgraph main_graph内に記載されているサイズを入力データのサイズとする

# 推論
output = sess.run(
    None,
    {"input.1":input_image} # 上記でグラフの構造を表示したときのgraph main_graph内に記載されている変数を入力変数とする
)

print("推論されたカテゴリ:", output[0].argmax(1))

まとめ

　本記事では、PyTorchで作成したモデルの保存方法と読み込み方についてまとめました。下記の3種類の方法を適切に使い分けられるようにしていきたいです。

モデルの重みだけを保存する
モデルの重みだけでなく構成も保存する
1. PyTorchでしか読み込めない方法
2. PyTorch以外でも読み込める方法

2024-06-13

【Python】f文字列の書式指定でハマった

エンジニアリング

はじめに

　Pythonのf文字列の書式指定でハマったので、記録しておきます。

ハマったこと

　下記のコードでprintしたときに、想定と異なる挙動をしました。

print(f"{0.123456789: <010f}")
# ->「0.123457」 と表示された

　書式指定が<010fなので、左詰め・桁数の不足分は0埋め・全体で10桁（小数点も1桁とカウント）・小数点の有効数字6桁の0.12345700と表示されると思っていました（図１）。しかし、実際は0.123457と表示されてしまいました。

想定と異なる挙動をした理由

　理由はシンプルで、:と<010fの間に半角スペースが含まれていたためです。下記のように、半角スペースを除くと想定した挙動になりました。

print(f"{0.123456789:<010f}")
# ->「0.12345700」 と表示された

　半角スペースが含まれると想定した挙動にならない理由まではわかりませんでした。しかし、半角スペースを除くと想定した挙動になったので、とりあえず良しとしています。