目次
はじめに
現在、ディープラーニング(DL)は様々な分野で使われています。今流行の生成AIなんて、DLの塊です。また、私の所属する会社で行われているセキュリティネットワークの研究においても、DLは重要な意味合いを持っています。
その一方で、私自身ちゃんとDLについて過去に勉強してきたことがありません。したがって、私にとってDLは、データサイエンスにおける超重要な技術であるにもかかわらず、自信を持って語ることができない技術の一つになっています。そこで2023年度の下期は、体系的にDLを学ぶべくなっとく!ディープラーニングを読むことにしました。
本記事では、自分が躓いた第4章について説明していきたいと思います。
第4章の理解の仕方
第4章のテーマは、勾配降下法です。私自身は本書の説明だけでは理解ができず、ネットでググった数式を見ながら本書を読み解きました。私は下記の流れで第4章を理解しました。
- 勾配降下法の更新式を理解する
- データが一つの場合の勾配降下法の更新式を、実際に導出する
- 本書に書かれているコードと照らし合わせる
勾配降下法の更新式を理解する
図1のような最もシンプルなニューラルネットワークを考えます。
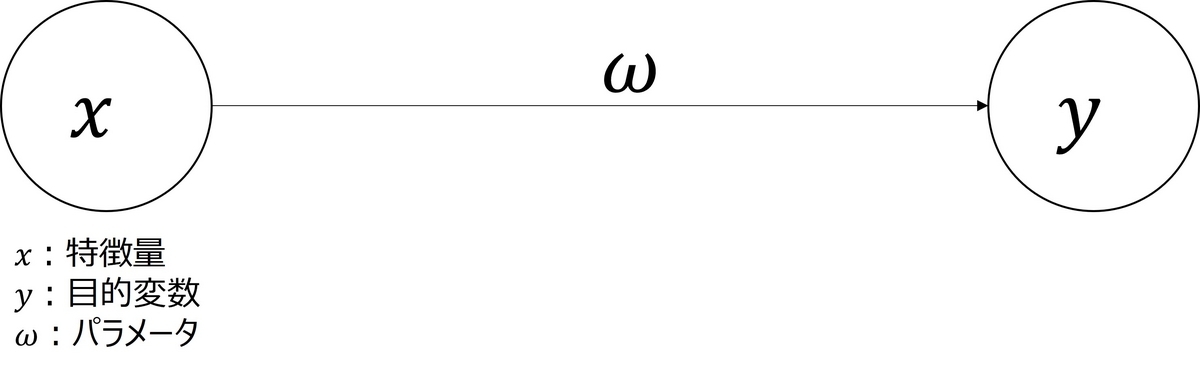
このとき、の勾配降下法の更新式は、
となります。ただし、は更新後のパラメータ、
は更新前のパラメータ、
は学習率、
は損失関数です。
勾配降下法の更新式がこのような形になっている理由については、勾配降下法が分かりやすかったです。
大事なことは、パラメータを更新する方向をで定め、更新する大きさを学習率
で定めるということです。
データが一つの場合の勾配降下法の更新式を、実際に導出する
本書では、損失関数としてMean Square Error(MSE)を使っています。また、図1より予測値は
となります。したがって、
となります。したがって、更新式は、
となります。
本書に書かれているコードと照らし合わせる
本書のp. 56, 57に書かれているコードと更新式を照らし合わせたものが表1です。
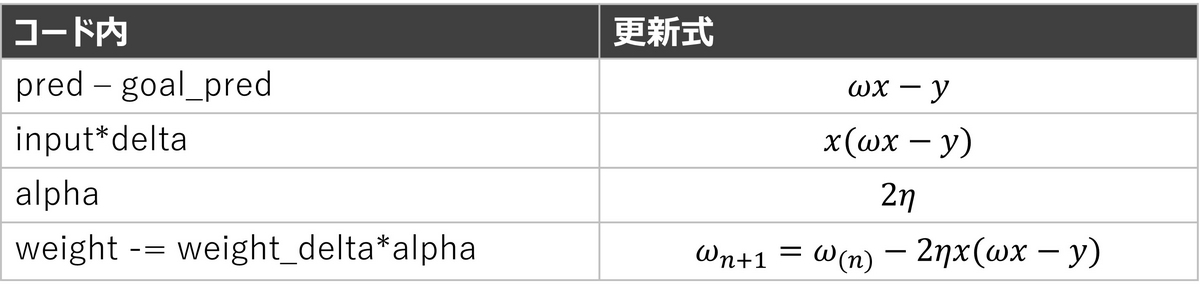
まとめ
本書の第4章では、勾配降下法について説明されています。繰り返しになりますが、私は下記の手順で理解しました。
- 勾配降下法の更新式を理解する
- データが一つの場合の勾配降下法の更新式を、実際に導出する
- 本書に書かれているコードと照らし合わせる
これにより、特徴量・目的変数が1次元の1層のニューラルネットワークについて、パラメータの学習の仕方を理解することができました。 これで、特徴量・目的変数が複数次元で、複数層のニューラルネットワークについて勉強していく準備ができたと考えています。
